Number Definition, Types and Examples

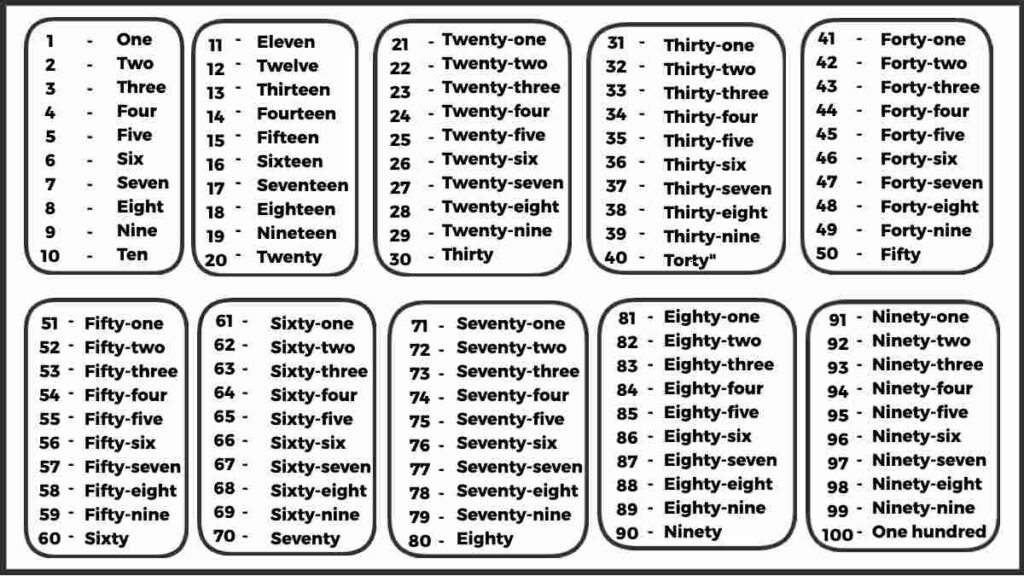
If you are going to read all the information about the numbers on this page, then definitely read the post completely.

On the previous page, we have shared the information about Number System, which are the basis of mathematics, read that post as well.

Let us read and understand all the information about numbers on this page.

What is the Number Called

Those Mathematical Objects Which are used for Counting, Measuring and Naming are Called Numbers.

There are Total 10 Numbers (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) in Arithmetic. With the Help of Which big Numbers are Formed.

Zero is Considered as a Whole Number, the value of the number which is followed by zero increases 10 times.

As :-

• Placing 0 after 2 makes it 20 (twenty).
• Putting 0 after 5 becomes 50 (fifty).
• Putting 00 behind 10 becomes 1000 (one thousand).
• Putting 000 behind 20 becomes 20,000 (twenty thousand).
• Putting 0000 behind 500 becomes 50,00000 (fifty lakhs).

What is Number System

0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are called numbers. Numbers are made up of Digits. The way of writing numbers is called number system.

There are two systems of writing a number.

• Decimal system
• International system

1. Decimal System

The decimal system is also known as the Indian Arabic system.

By looking at the table below, you can clearly understand that by writing unit, ten hundredth, thousand, ten thousand, lakh, ten lakh, crore, ten crore, billion, ten billion etc. from right to left respectively, place the numbers below it. Let’s write on

Like :- Eighty Billion, Thirty Two Crore, Five Lakh, Six Thousand, Nine Hundred and Twenty Four.

Writing Place Value into a table

Ten Billion	Arab	One hundred million	Ten million	Million	Lakh	Ten thousand	Thousand	Hundreds	Ten	Unit
8	0	3	2	0	5	0	6	9	2	4

Number in Digits = 80,32,05,06,924

2. International System

In the international system, you can clearly understand by looking at the table below, in this from right to left and respectively unit, tens, hundreds, thousand, ten thousand, hundred thousand, million, ten million, hundred million, billion, ten billion, hundred billion etc. .

Example : Fifty billion, seven hundred and ninety million, eight hundred and five thousand, four hundred and four

Tabulating the international system

Hundred Billion	Ten Billion	Billion	Hundred Million	Ten Million	Milium	Hundred Thousand	Ten Thousand	Thousand	Hundreds	Ten	Unit
0	5	0	7	9	0	8	0	5	4	5	4

Number in digits = 50, 790, 805, 454

Racial Value of Digits in a Number

Any Number Which is made up of two or more digits has its own value.

Face Value :- The face value of a number does not depend on its place in a number, the actual value of that number is called face value.

For example :- The caste value of 7 in 5,42,73,679 is 7 only, whether it is 7 in ten’s place or 7 in ten thousand’s place.

Place Value of Digits in a Number

Place Value :- The place value of a digit depends on its place in a number.

For example :- Place value of 8 in 56783 = 8 × 10 = 80

Note :- The caste value and local value of zero (0) is always 0.

For more information read the post on place value and caste value.

Types of Numbers

There are 12 Types of Numbers.

1. Natural Numbers → 1, 2, 3, 4, 5, ………
2. Even Number → 2, 4, 6, 8, 10, ………
3. Odd Number → 1, 3, 5, 7, 9, ………
4. Integers → -3, -2, -1, 0, 1, 2, 3, ………
5. Whole Numbers → 0, 1, 2, 3, 4, ………
6. Composite Number → 4, 6, 8, 9, ………
7. Prime Numbers → 2, 3, 5, 7, 11, ………
8. Co Prime Numbers → (5, 7) , (2, 3)
9. Rational Numbers → √4, 7/5, 2/3, 3
10. Irrational Numbers → √5, √7, √11, √13
11. Real Numbers → √4, √11, 4/7
12. Unreal Numbers → √-6, √-5, √-29

Below we will read and understand the 12 types of numbers in detail.

1. Natural Number

All the numbers used in counting are called natural numbers. 0 is not included in the natural numbers. Natural Numbers start from 1 and go to infinity.

For Example :- 1, 2, 3, 4, 5, 6, 7, 8, 9……………infinite

2. Even Number

Such natural numbers which are exactly divisible by 2 are called even numbers.

Example :- 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…….………infinite

3. Odd Number

Natural numbers which are not exactly divisible by 2 are called odd numbers.

Example :- 1, 3, 5, 7, 9, 11, ……………infinite

4. Integer Number

Integer Number, Integers are numbers made up of positive, negative and zeros.

Example :- -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5……………..………infinite

There are three types of integer numbers.

• Positive Number
• Negative Number
• Neutral Integer

(a). Positive numbers :- All positive numbers from one to infinity are positive integers.

(b). Negative numbers :- All negative numbers from 1 to infinity are positive integers.

(c). Neutral Integer :- Such an integer on which no flow of positive and negative sign is read and it is zero.

5. Whole Number

When zero is included in a natural number, it becomes a whole number. Whole numbers start from 0 and go to infinity.

Example :- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9……….………infinite

6. Composite Number

A natural number which is divisible by at least one other number other than itself and 1 is called a composite number.

For example :- 4, 6, 8, 9, 10, 12, 14, 16, 18, 20……..………infinite

7. Prime Number

Natural numbers that are divisible only by themselves and 1 and not by any other number are called prime numbers.

For example :- 2, 3, 5, 11, 13, 17, ………

8. Co-prime Number

The set of at least 2 prime numbers whose HCF is 1 is called co-prime number.

For example :- (5, 7) , (2, 3)

9. Rational Number

All numbers that can be written in the form of p/q. They are called rational numbers.

(q denominator should not be zero)

For example :- 5, 2/3, 11/4, √25

10. Irrational Number

Numbers that cannot be written in the form of p/q are usually written inside (√). And their perfect square root never comes out is called irrational number.

Example:- √3, √7, √11, √17, √117, √223

Note :- (Pi is an irrational number.)

11. Real Number

Real numbers are obtained by writing rational and irrational numbers together.

For Example :- 2/5, 4/7, 11/13, √5, √11, √47,

12. Unreal Number

It is an imaginary number that does not have a real number. Unreal numbers or imaginary numbers are represented by units.

For Example :- √- 2, √-4, √-12, √-17, √-107 etc.

Important Point :-

• 1 is neither a composite number nor a prime number.
• 2 is the smallest prime number.
• 2 is such a number that it is prime as well as even.
• All prime numbers are odd.
• There are 9 prime numbers from 1 to 25.
• There are 15 prime numbers from 1 to 50.
• There are 10 prime numbers from 50 to 100.
• There are 25 prime numbers from 1 to 100.
• Adding any two or more even numbers always gives an even number.
• If an odd number is added to an even number, an odd number will always be obtained.
• If two odd numbers are added together, there will always be an even number.
• Any number raised to any number of powers will always result in an even number.
• Any odd number raised to the power will always result in an odd number.

largest and smallest numbers :-

• The smallest one digit number is 1.
• The largest one digit number is 9.
• The smallest two digit number is 10.
• The largest two digit number is 99.
• The smallest three digit number is 100.
• The largest three digit number is 999.
• The smallest number of four digits is 1000.
• The largest four digit number is 9999.
• The smallest number of five digits is 10000.
• The largest five digit number is 99999.

Number Based Questions and Answers

Q.1 What is the place value of 7 in the number 987653?
A.8
B.8926
C.7000
D.8000

Solution:- According to the question,
Place value of 7 in the number 987653 = 7 × 1000
place value = 7000
Ans. 7000

Q.2 What is the place value of 5 in 0.06537?
A.5
B.5/100
C.5/1000
D.65/1000

Solution:- According to the question,
place value of 5 in 0.06537
place value = 0.005
place value = 5/1000
Ans. 5/1000

Q.3 What is the place value of each number in 678954?

Solution:- In 678954,
Place value of 4 = 4 × 1 = 4.
Place value of 5 = 5 × 10 = 50.
The place value of 9 = 9 × 100 = 900.
Place value of 8 = 8 × 1000 = 8000.
The place value of 7 = 7 × 10000 = 70000.
The place value of 6 = 6 × 100000 = 600000.

Q.4 What is the numerical value of 5 in 45678?

Solution:- According to the question,
The caste value of 5 in the number 45678 = 5
Ans. 5

Q.5 What is the caste value of each number in 67543?

Solution:- In 67543,
Caste value of 6 = 6
Caste value of 7 = 7
Caste value of 5 = 5
Caste value of 4 = 4
Caste value of 3 = 3

Q.6 What are the difference between the place values ​​of 6 in 7682463?
A.699940
B.599940
C.682933
D.599993

Solution:- According to the question,
Local value and caste value of 7682463
Place value of 6 = 600000
Caste value of 6 = 60
Difference in place value of 6 = 600000 – 60
difference = 599940
Ans. 599940

Q.7 On dividing 7765 by a number, the quotient is 45 and the remainder is 25. What are the divisors?
A. 165
B. 172
C. 175
D. 180

Solution:- According to the question,
Formula :- Divisor = (Dividend – Remainder) / Quotient
Divisor = (7765 – 25)/45
denominator = 172
Ans. 172

Q.8 What will be the unit’s digit in 43 × 44 × 45 ……… × 48?
A. 3
B. 1
C. 2
D. 0

Solution:- According to the question,
Number of unit’s digit in 43 × 44 × 45 × 47 × 48
Product = 3 × 4 × 5 × 6 × 7 × 8 = 20160
Unit Present Required Marks = 0
Ans. 0

Q.9 The unit’s digit in the product (2467)¹⁵³ × (341)⁷² × (225)⁷²¹ is?
A. 1
B. 3
C. 5
D. 7

Solution:- According to the question,
(2467)¹⁵³ × (341)⁷² × (225)⁷²¹
Unit’s digit in (2467)¹⁵³
Unit’s digit in the remainder of (2467)¹⁵³⁄₄
Unit digit in (7)¹ = 7
(341) Unit’s digit in⁷² = 1
(225) Unit’s digit in⁷²¹ = 5
Hence, required unit’s digit = 7 × 1 × 5
Required unit digit = 35
Unit digit = 5
Hence the unit digit will be 5.
Ans. 5

Q.10 The digit in the unit’s place of the number 17¹⁹⁹⁹ + 11¹⁹⁹⁹ − 7¹⁹⁹⁹ is?
A. 1
B. 3
C. 5
D. 8

Solution:- According to the question,
17¹⁹⁹⁹ + 11¹⁹⁹⁹ − 7¹⁹⁹⁹
Unit’s digit in 17¹⁹⁹⁹
(17)The unit’s digit in the remainder of ¹⁹⁹⁹⁄₄
(7) Unit’s digit in ³ = 3
(11)Unit’s digit in ¹⁹⁹⁹ = 1
(7)Unit’s digit in ¹⁹⁹⁹ = 3
Thus, required unit digit = 3 + 1 − 3
Unit digit = 4 − 3
Unit digit = 1
Hence the unit digit will be 1.
Ans. 5

Q.11 A number between 100 and 1000 will always be divided by the number obtained by subtracting the sum of its digits.
A. From 3
B. since 6
C. 5 to
D. since 12

Solution:- According to the question,
numbers between 100 and 1000
= 100x + 10y + z
[where 0 ≤ x, y, z ≤ 9]
(100x + 10y + z) – (x + y + z)
= 99x + 9y
= 9 (11x + y)
= multiple of 9
Hence the number is a multiple of 9 which will also be a multiple of 3.
Ans. 3

Q.12 How many numbers are there between 200 and 600 which are exactly divisible by 4, 5 and 6?
A.5
B.8
C.6
D.9

Solution:- According to the question,
LCM of 4, 5 and 6 number = 60
Smallest number greater than 200 which is divisible by 60 – 240
Largest number between 200 and 600 which is divisible by 60 = 540
Agreed,
Required number = n
540 = 240 + (n – 1) 60
540 = 240 + (n – 1) 60
(n – 1) = (540 – 240)/60
(n – 1) = 300/60
(n – 1) = 5
n = 5 + 1
n = 6
Ans. 6

Q.13 If a : (b + c) = 1 : 3 and c : (a + b) = 5 : 7, then b : (c + a) is equal to?
A.1/2
B.2/3
C.5/2
D.2/1

Solution:- According to the question,
a : (b + c) = 1 : 3
a/(b + c) = 1/3 or a = (b + c)/3
and c : (a + b) = 5 : 7
c/a + b = 5/7
7c = 5a + 5b
7c = 5 × b + c/3 + 5b
21c = 5b + 5c + 15b
c = 20b/16
c = 5b/4
b/(c + a) = b/(5b/4 + 3b)/4
b/(c + a) = b/(5b + 3b)/4
b/(c + a) = b/(8b/4)
b/(c + a) = b/2b
b/(c + a) = 1/2
Ans. 1/2

Q.14 9 | 3 − 5 |-5 | 4 | ÷ 10 / -3(5) −2 × 4 ÷ 2 Find the value?
A.⁹⁄₁₀
B.⁻⁸⁄₂₇
C.⁻¹⁶⁄₉₉
D.⁴⁄₇

Solution:- According to the question,
9 | 3 − 5 |-5 | 4 | ÷ 10 / -3(5) −2 × 4 ÷ 2
9 × 2 × -5 × 4 × ÷ 10 / -3 × (5) −2 × 2
18 × -5 × 4/10 / -15 – 4
16/-19
Ans. ⁻¹⁶⁄₉₉

Q.15 If x/y, then the value of x² + y²/x² ⁻ y² is?
A. ³⁶⁄₂₅
B.²⁵⁄₃₆
C.⁶¹⁄₁₁
D.¹¹⁄⁶¹

Solution:- According to the question,
x² + y²/x² ⁻ y²
(x/y)² + 1/(x/y)² – 1
(x/y)² + 1/(x/y)² – 1 [divided by y²]
(6/5)² + 1/(6/5)² – 1
(36/25 + 1)/(36/25 – 1)
(36 + 25)/25 / (36 – 25)/25
61/25 / 11/25
61/25 × 25/11
61/11
Ans. ⁶¹⁄₁₁

FAQ

Must Read :

• Square Root
• Cube Root
• Tables 1 to 100

Hope you have liked the post of numbers, if you have liked the information about numbers, then definitely share it with your friends. Thank you.