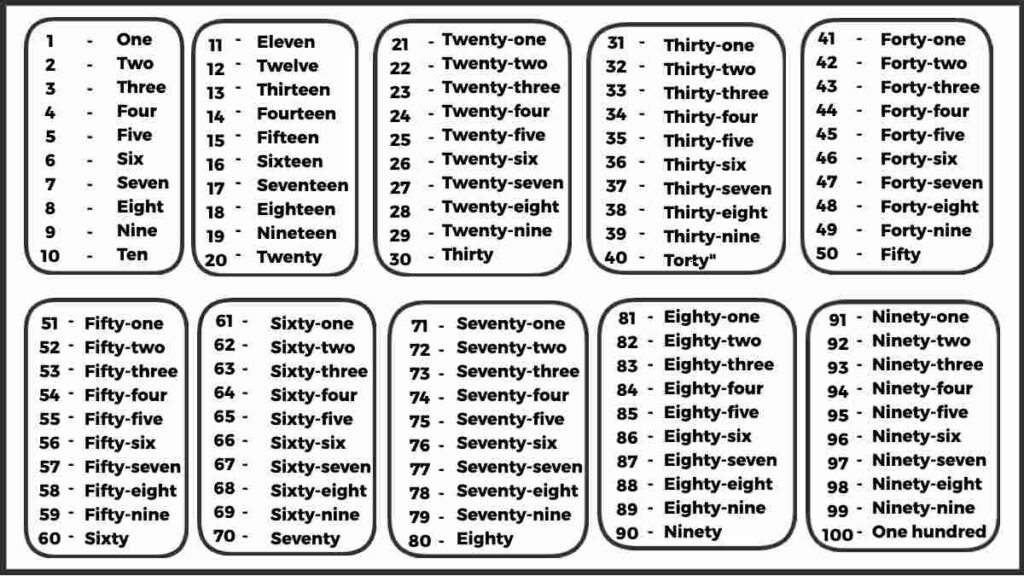
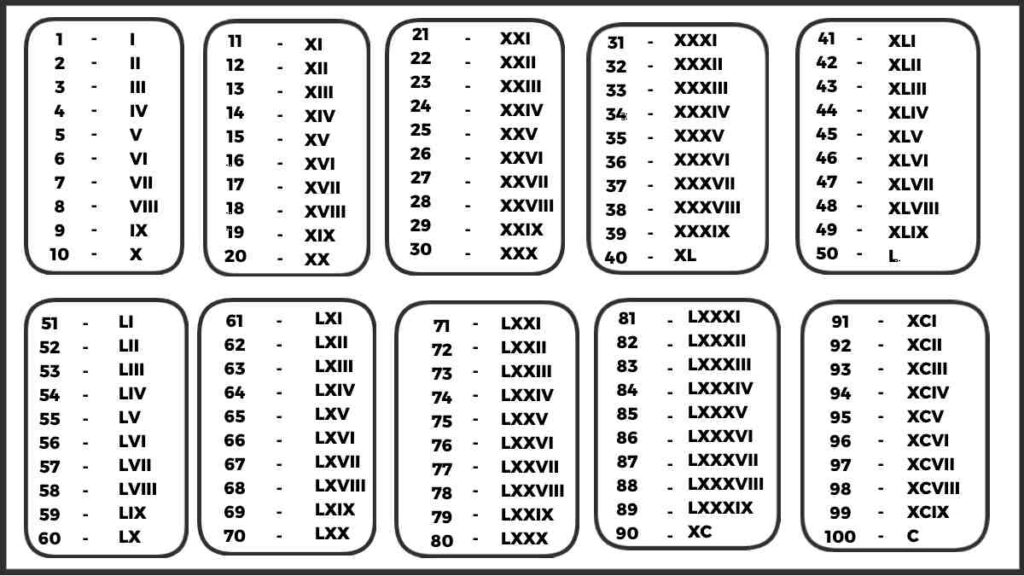
If you are going to read the information about integer number on this page, then definitely read the article completely.
On the previous page, we have shared the information about Even Number and Odd Number, so definitely read the post.
Let us read and understand the example of what is called an integer number on this page with its solution.
What is an Integer Number
The Numbers made up of Positive, Negative and zero are called Integer Numbers.
Ex : -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5
Integer Number Types
There are three types of Integer Numbers.
- Positive Numbers
- Negative Numbers
- Neutral Integer
1. Positive Integer
All positive numbers from one to infinity are called positive integers.
Any integer number that does not have any sign of positive or negative in front of it, such numbers are called positive integers.
Like :- 1, 2, 3, 4, 5, 6, 7, 8, 9, …………..
All these numbers come under positive integers.
Positive Numbers are Located to the right of zero on the integer number line, so these numbers will come under positive integers.
2. Negative Integer
All negative numbers from 1 to infinity are called negative integers.
Negative integer numbers are preceded by a negative sign. Negative numbers are located to the left of zero on the number line. The numbers which are less than zero are called negative integers.
Like :- -1, -2, -3, -4, -5, -6, -7, -8, -9 ……..……∞
All these numbers come under negative integers.
3. Indifferent Integers
An integer that is neither a positive nor a negative integer. are called neutral integers. It comes under zero integers.
Like :- 3, -2, -1, 0, 1, 2, 3, ……………∞
Properties of Integers
There are two types of properties of integer numbers.
- Properties of Subtraction of Integers
- Multiplication of Integer Numbers
1. Properties of Subtraction of Integers
There are five types of properties of subtraction of integers.
(a). Closed Under Yoga
Integers follow the closure rule under addition.
That is, according to this rule, on adding any two integers, the result obtained is an integer only.
- 2 + 2 = 4
- 5 + 5 = 10
- 10 + 10 = 20
- 50 + 50 = 100
Here 4, 10, 20 and 50 are whole numbers.
(b). Closed Under Subtraction
Integer numbers obey the closure rule under subtraction. According to this, when any two integers are subtracted from each other, the result obtained will also be an integer number.
As :-
- 8 – 4 = 4
- 24 – 12 = 12
- 50 – 24 = 26
- 100 – 86 = 14
Here 4, 12, 26 and 14 are whole numbers.
(c). Commutative Properties
It follows the commutative rule for adding integer numbers. That is, if two integers are added in any order, the result remains the same.
As :-
- 5 + 3 = 8
- 3 + 5 = 8
Both the results are equal so they follow commutative rule.
(d). Associative Properties
Addition and subtraction of integers follow the associative property.
a + (b + c) = (a + b) + c
(e). Additive Identity
Zero is an additive identity for whole numbers.
a + 0 = a = 0 + a
2. Multiplication of integer numbers
First mathematician who tried to prove that (–1) × (–1) = 1 in his book “Ankitung zur Algebra” in 1770 AD.
As :-
- (-2) × (-2) = 4
- (-5) × (-7) = 35
- (-5) × (-8) = 40
- (-9) × (-5) = 45
(a). Closed Under Multiplication
Integers are closed under multiplication. A × b is an integer for all integers a and b.
As :-
2 × 5 = 10
4 × 6 = 24
6 × 7 = 42
8 × 8 = 64
(b). Commutativity of Multiplication
Integer numbers show commutativity with respect to multiplication. In general, commutativity of multiplication for any two integers a and b
a × b = b × a
As :-
4 × 5 = 20
5 × 4 = 20
(c). Multiply by Zero
When an integer number is multiplied by zero, zero is obtained as the product.
a × 0 = 0 × a = 0
As :-
2 × 0 = 0
7 × 0 = 0
(d). Multiplicative Identity
1 is the multiplicative identity for whole numbers.
a × 1 = 1 × a = a
(e). Multiplication Associative Property
This multiplication obeys the associative property.
(a × b) × c = a × (b × c)
Critical Points of Integer Numbers
- The numbers 0, 1, -1, 2, -2, 3, -3, ……….…….∞ are called integer numbers.
- The numbers +1, +2, +3, +4, ……………∞ are called positive integers.
- The numbers -1, -2, – 3, – 4, ……………………….∞ are called integers.
- The numbers 0, + 1, + 2, + 3, + 4 are called non-negative integers.
- Non-negative integers are called whole numbers.
All positive integers lie to the right of 0 on the number line and all negative integers lie to the left of 0 on the number line.
Two integers whose sum is zero are called additive inverses of each other. They are also said to be negative of each other.
Addition, Subtraction, Multiplication and Division of Integers
Rule of Addition of Two Integers
- (-) + (-) = (+)
- (+) + (+) = (+)
- (-) + (+) = (-)
- (+) + (-) = (-)
Sum of Integers with Same Sign
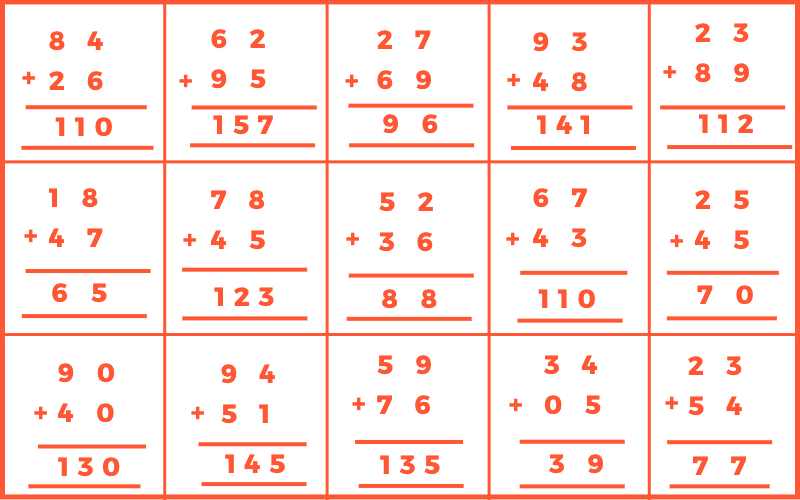
Addition of Integers with Different Signs

law of Product of Two Integers
(-) (-) = (+)
(+) (+) = (+)
(-) (+) = (-)
(+) (-) = (-)
Product of Integers with the Same Sign
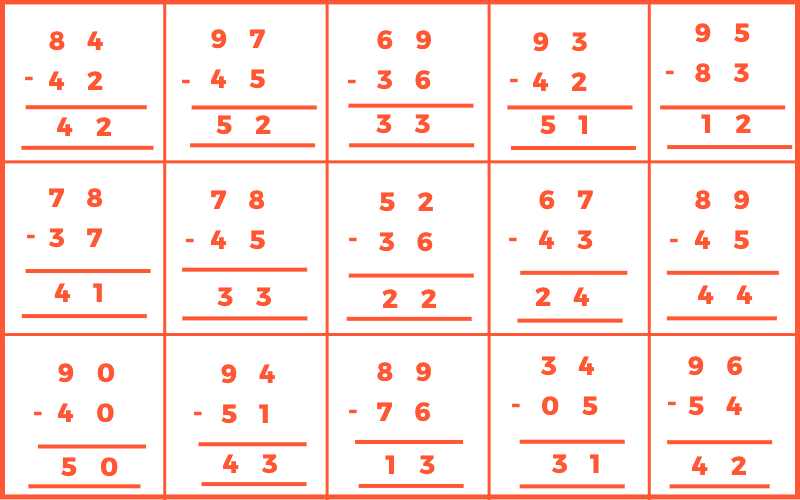
Product of Integers with Different Signs
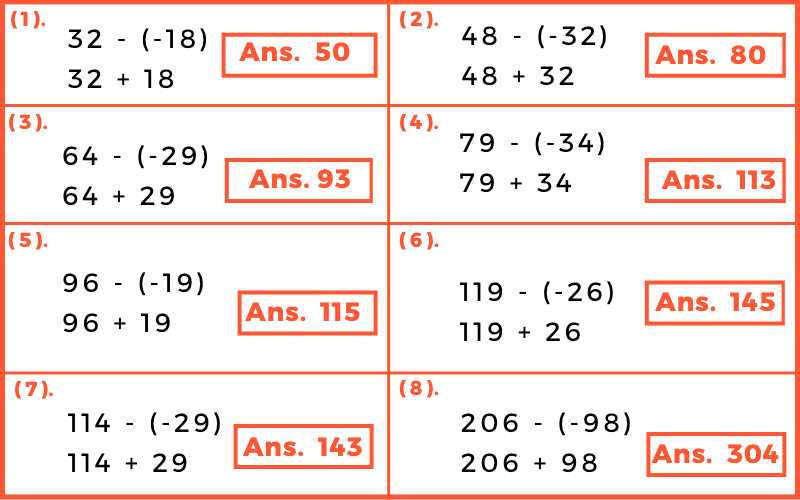
Law of Product of Two Integers
- (-) × (-) = (+)
- (+) × (+) = (+)
- (-) × (+) = (-)
- (+) × (-) = (-)
Product of Integers with the Same Sign

Product of Integers with Different Signs

Rules for Division of Two Integers
- (-) ÷ (-) = (+)
- (+) ÷ (+) = (+)
- (-) ÷ (+) = (-)
- (+) ÷ (-) = (-)
Division of Integers with the Same Sign
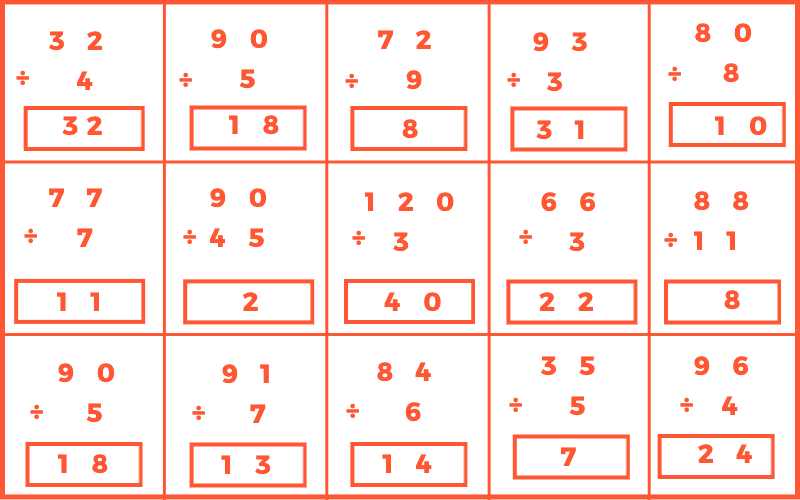
Division of Integers with Different Signs

Integer Number Question Answer
Q.1 Find the sum of the pairs of integers (-8), (-4)?
(A). 12
(B). -12
(C). 8
(D). -4
Solution:- According to the question,
-8 and -4 both have negative signs.
So -8 + (-4) = -(8 + 4)
Ans. -12
Q.2 Find the sum of the pairs of integers (+8), (– 2)?
(A). 10
(B). -10
(C). 6
(D). -6
Solution:- According to the question,
The signs of +8 and -2 are opposite.
So +8 + (-2) = 8 – 2
Ans. 6
Q.3 subtract 4 from (-12)?
(A). 4
(B). -4
(C). 16
(D). -16
Solution:- According to the question,
The additive inverse of 4 is = – 4.
So -12 – 4
= -12 + (-4)
= -(12 + 4)
= -16
Ans. -16
Q.4 Subtract (-8) from (-25)?
(A). 8
(B). -8
(C). 17
(D). -17
Solution:- According to the question,
The additive inverse of -8 = +8.
So -25 – (-8)
= -25 + (+8)
= -25 + 8
= -17
Ans. 17
Q.5 How many integers are there between (-9) and (-4)?
(A). 6
(B). 8
(C). 4
(D). 10
Solution:- According to the question,
The integers between -9 and -4 are -8, -7, -6 and -5.
So there are 4 integers between -9 and -4.
Q.6 Write the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 in that order and put ‘+’ or ‘-‘ in between them in such a way that 5 is obtained?
(A). 3
(B). 5
(C). 7
(D). 9
Solution:- According to the question,
0 + 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9
= (0 + 1 + 3 + 5 + 7 + 9) – (2 + 4 + 6 + 8)
= 25 – 20
= 5
Ans. 5
Ans. An integer is a whole number (not a fractional number) that can be positive, negative, or zero.
Examples of integers are : -5, 1, 5, 8, 97, and 3,043. Examples of numbers that are not integers are: -1.43, 1 3/4, 3.14, .09, and 5,643.1.
Ans. Integers are numbers which cannot be decimals or fractions. They are either whole numbers or negative numbers. Some examples are: 2, 7, 0, -9, -12, etc.
Ans. How do we know that √7 is irrational? For a start, 7 is a prime number, so its only positive integer factors are 1 and 7 .
Ans. Every integer is a Real number and Rational number but not Irrational numbers and natural numbers. Therefore, every integer is a real number and a rational number.
Ans. If we want to represent the non-negative integers we’d use the symbol Z+. So, Z+ = {0, 1, 2, 3,…}. If we want to represent just the positive integers we’d use the symbol P.
Hope you have liked the information about integer numbers.
Comment with any questions related to integers. Thanks.