Square Root 1 to 100

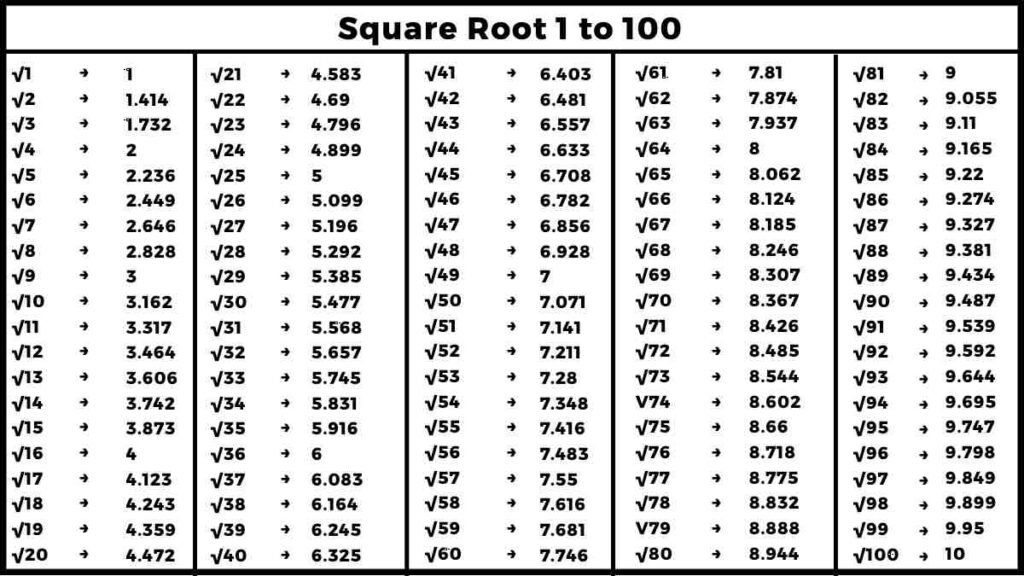
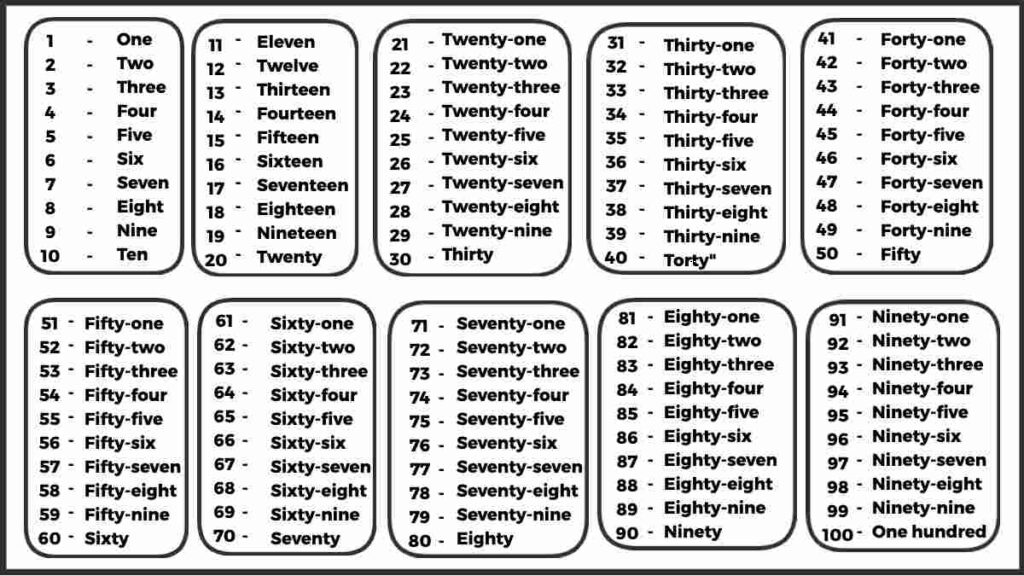
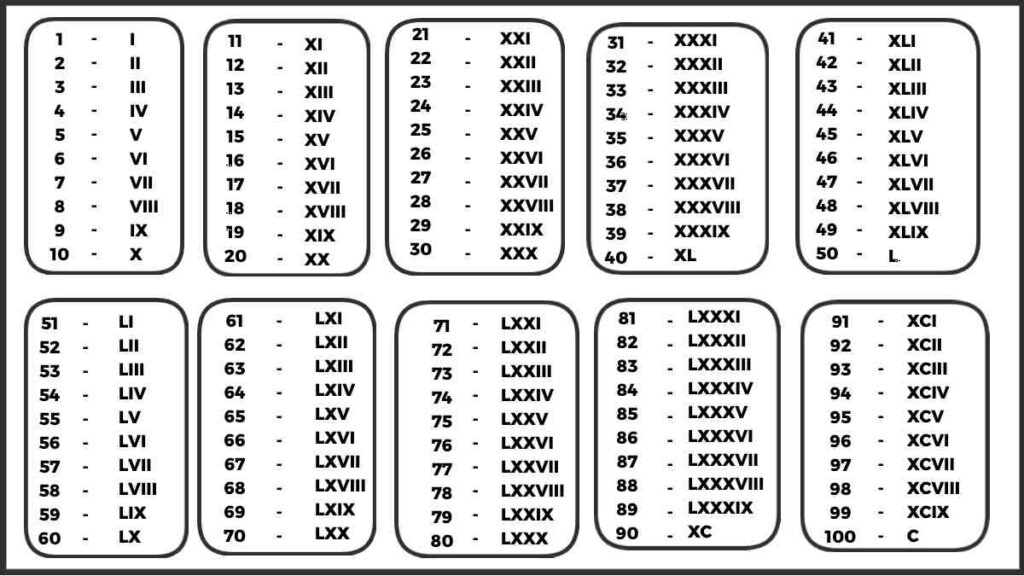
On this page, you will find Square Root 1 to 100, by reading which you will be able to solve math problems easily.

On the previous page, we had shared the information of Squares From 1 to 100, so read that article as well, let us read and understand the information of Square Root 1 to 100 today.

Square Root 1 to 100

Number (N)	Square (N²)	Square root (√N)
1	1	1
2	4	1.414
3	9	1.732
4	16	2
5	25	2.236
6	36	2.449
7	49	2.646
8	64	2.828
9	81	3
10	100	3.162
11	121	3.317
12	144	3.464
13	169	3.606
14	196	3.742
15	225	3.873
16	256	4
17	289	4.123
18	324	4.243
19	361	4.359
20	400	4.472
21	441	4.583
22	484	4.69
23	529	4.796
24	576	4.899
25	625	5
26	676	5.099
27	729	5.196
28	784	5.292
29	841	5.385
30	900	5.477
31	961	5.568
32	1024	5.657
33	1089	5.745
34	1156	5.831
35	1225	5.916
36	1296	6
37	1369	6.083
38	1444	6.164
39	1521	6.245
40	1600	6.325
41	1681	6.403
42	1764	6.481
43	1849	6.557
44	1936	6.633
45	2025	6.708
46	2116	6.782
47	2209	6.856
48	2304	6.928
49	2401	7
50	2500	7.071
51	2601	7.141
52	2704	7.211
53	2809	7.28
54	2916	7.348
55	3025	7.416
56	3136	7.483
57	3249	7.55
58	3364	7.616
59	3481	7.681
60	3600	7.746
61	3721	7.81
62	3844	7.874
63	3969	7.937
64	4096	8
65	4225	8.062
66	4356	8.124
67	4489	8.185
68	4624	8.246
69	4761	8.307
70	4900	8.367
71	5041	8.426
72	5184	8.485
73	5329	8.544
74	5476	8.602
75	5625	8.66
76	5776	8.718
77	5929	8.775
78	6084	8.832
79	6241	8.888
80	6400	8.944
81	6561	9
82	6724	9.055
83	6889	9.11
84	7056	9.165
85	7225	9.22
86	7396	9.274
87	7569	9.327
88	7744	9.381
89	7921	9.434
90	8100	9.487
91	8281	9.539
92	8464	9.592
93	8649	9.644
94	8836	9.695
95	9025	9.747
96	9216	9.798
97	9409	9.849
98	9604	9.899
99	9801	9.95
100	10000	10

Value of Square Roots from 1 to 100

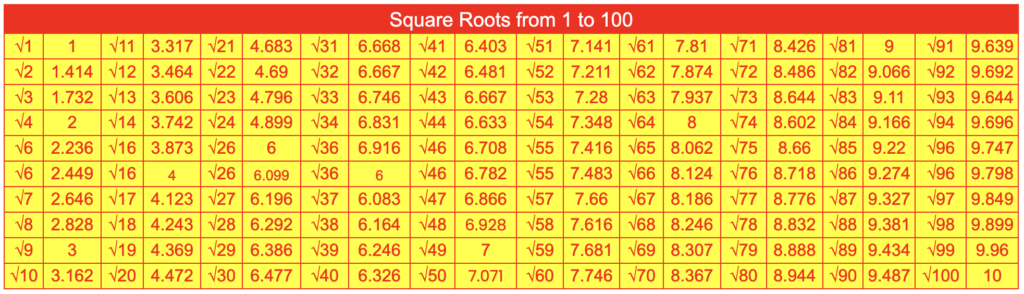
Square Roots from 1 to 10

√1	1
√2	1.414
√3	1.732
√4	2
√5	2.236
√6	2.449
√7	2.646
√8	2.828
√9	3
√10	3.162

Square Roots from 11 to 20

√11	3.317
√12	3.464
√13	3.606
√14	3.742
√15	3.873
√16	4
√17	4.123
√18	4.243
√19	4.369
√20	4.472

Square Roots from 21 to 30

√21	4.683
√22	4.69
√23	4.796
√24	4.899
√2	5
√26	5.099
√27	5.196
√28	5.292
√29	5.386
√30	5.477

Square Roots from 31 to 40

√31	6.668
√32	6.667
√33	6.746
√34	6.831
√35	6.916
√36	6
√37	6.083
√38	6.164
√39	6.246
√40	6.326

Square Roots from 41 to 50

√41	6.403
√42	6.481
√43	6.667
√44	6.633
√45	6.708
√46	6.782
√47	6.866
√48	6.928
√49	7
√50	7.071

Square Roots from 51 to 60

√51	7.141
√52	7.211
√53	7.28
√54	7.348
√55	7.416
√56	7.483
√57	7.66
√58	7.616
√59	7.681
√60	7.746

Square Roots from 61 to 70

√61	7.81
√62	7.874
√63	7.937
√64	8
√65	8.062
√66	8.124
√67	8.186
√68	8.246
√69	8.307
√70	8.367

Square Roots from 71 to 80

√71	8.426
√72	8.486
√73	8.644
√74	8.602
√75	8.66
√76	8.718
√77	8.776
√78	8.832
√79	8.888
√80	8.944

Square Roots from 81 to 90

√81	9
√82	9.066
√83	9.11
√84	9.166
√85	9.22
√86	9.274
√87	9.327
√88	9.381
√89	9.434
√90	9.487

Square Roots from 91 to 100

√91	9.639
√92	9.692
√93	9.644
√94	9.696
√95	9.747
√96	9.798
√97	9.849
√98	9.899
√99	9.96
√100	10

Examples

Example 1. Find the value of x, if x√100 = 2000.

Solution : Given that, x√100 = 2000
As we know, the square root of 100 is 10.
I.e., √100 = 10
Hence, x(10) = 2000
10x = 2000
x = 2000/10 
x = 200
Therefore, the value of x is 200.

Example 2. Determine the value of x, if x = 2√49

Solution : Given : x = 2√49
We know that, √49 = 7
Hence, x = 2(7)
= 14 Ans.

Example 3. If a circular tabletop has a radius of 70 inches. Find the area of the tabletop in sq. inches? [Use π = 3.14]

Solution : Area of circular tabletop = πr² 
= π (70)²
Using values from square 1 to 100 chart;
i.e. A = 4900π
= 4900 x 3.14
= 15386
Therefore, the area of the tabletop = 15386 inches².

Example 4. Find the area of a square window whose side length is 34 inches.

Solution : Area of square window (A) = Side²
i.e. A = 34²
= 1156
Therefore, the area of a square window is 1156 inches².

Example 5. Two square wooden planks have sides 30m and 42m respectively. Find the combined area of both the wooden planks?

Solution : Area of wooden plank = (side)²
⇒ Area of 1st wooden plank = 30²
= 900 m²
⇒ Area of 2nd wooden plank = 42²
= 1764 m²
Therefore, the combined area of wooden planks is 900 + 1764 = 2664 m²

Read More :
Discount	ProFit and Loss	Simple Interest
SimpliFication	LCM and HCF	Compound Interest

In this post you read the Square Root 1 to 100.

I hope you have liked this post.

If you liked the post of the class, then do share it on social media.