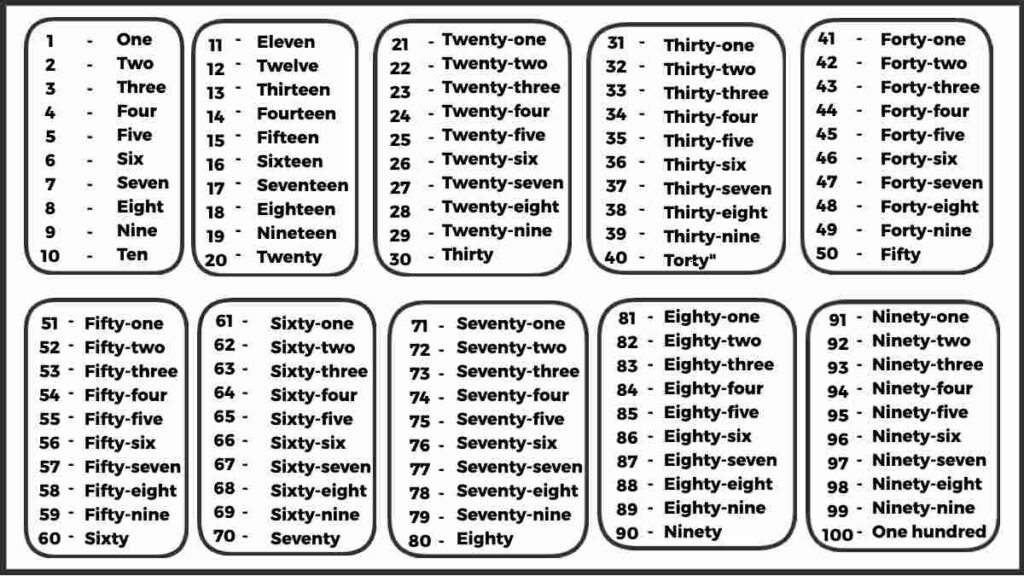
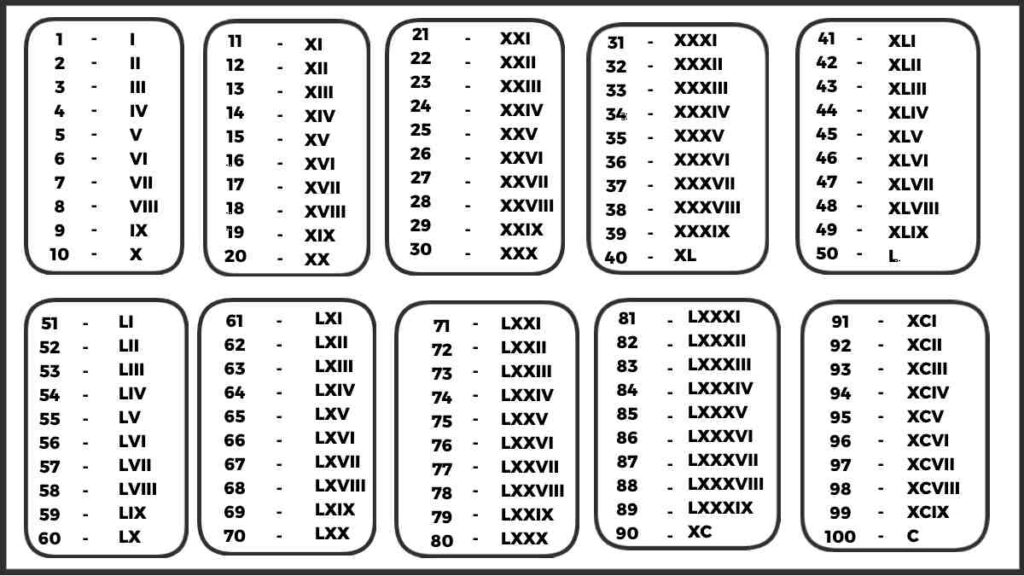
On this page, you are going to read Mathematics Formula which are necessary for government exams, so definitely read this article completely.
We have shared the information about Number System on the previous page, so read that post as well. Let us study maths formula today.
Mathematics Formula in English
Below you will find the formulas of the entire chapter of Mathematics subject, by reading which you will be able to solve any type of Mathematics questions easily.
1. Number System Formulas
- Sum of Natural Numbers = (first number + last number / 2) × n
- Sum of consecutive natural numbers = n(n + 1)/2
- N = (last number – first number / class interval) + 1
- Sum of Consecutive Even Numbers = n/2 (n/2 + 1)
- Sum of consecutive odd numbers = (n/2 + 1)²
- If the difference of two consecutive terms is same then sum = Number of terms (first term + last term)/2
- Sum of squares of consecutive natural numbers = n(n + 1)(2n + 1)/6
- Sum of cubes of consecutive natural numbers = [n(n + 1)/2]²
- Sum of even numbers from first to n = n(n + 1)
- sum of odd numbers from first to n = n²
- Quotient = dividend ÷ divisor (in complete division)
- Dividend = Quotient × Divisor (in complete division)
- divisor = dividend ÷ quotient (in complete division)
- Quotient = (Dividend – Remainder) ÷ Divisor (in incomplete division)
- Dividend = Quotient × Divisor + Remainder (in incomplete division)
- divisor = (dividend – remainder) ÷ quotient (in incomplete division)
Read More : Number System
2. Formulas for LCM and LCM
Least Common Multiple :- The ‘least common multiple’ of two or more numbers is the smallest number which is completely divisible by each of those given numbers.
For example :- The least common multiple of 3, 5, 6 is 30, because these three numbers can divide 30 respectively.
Common Multiple :- A number which is in two or more numbers. is exactly divisible by each of them, then that number is called the common multiple of those numbers.
For example :- The common multiple of 3, 5, 6 are 30, 60, 90 etc.
Greatest Common Factor :- ‘Greatest Common Factor’ is the maximum number which exactly divides the given numbers.
For example :- The greatest common factor of the numbers 10, 20, 30 is 10.
Common Factor :- A number that exactly divides each of two or more numbers.
For example :- The common factors of 10, 20, 30 are 2, 5, 10.
Factor and Multiple :- If a number m intersects another number n completely, then m is called a factor of n and n is called a multiple of m.
Methods of finding the least common multiple
Factorization method :- Prime factors of the given numbers are found and the factors are represented by power, then multiply the numbers of highest power.
As :-
LCM of 16, 24, 40, 42 ,
16 = 2 × 2 × 2 × 2 = 24
24 = 3 × 2 × 2 × 2 = 3 × 23
40 = 5 × 2 × 2 × 2 = 5 × 23
42 = 7 × 3 × 2 = 7 × 3 × 2
LCM = 24 × 3 × 5 × 7 = 16 × 105 = 1680
Division Method :-
This method can be understood by the following example.
Example :- LCM of 36, 48 and 80. S.
Hence LCM of 36, 48 and 80. S. = 2 × 2 × 2 × 2 × 3 × 3 × 5 = 720
In this the numbers can be divided by common prime divisors and this process is repeated till the remainder is one. The product of these prime divisors is the required LCM. Will happen.
Methods of Finding the Greatest Common Factor
Factorization Method :-
In this method, the prime factors of all the given numbers are done. And multiply the numbers which are common to all.
Like :- 28, 42 and 98’s M.S. ,
28 = 2 × 2 × 7
42 = 2 × 3 × 7
98 = 2 × 7 × 7
Mass of 28, 42 and 98. = 2 × 7 = 14
Division Method :-
In this method, the largest number is divided by the smallest of the given numbers, then the remaining remainder is divided into the denominator and this process is done till then.
As long as zero remains, then the last divisor is the HCF of the given numbers. If the number is three, then the obtained H.S. And do the same thing with the third number. They continue to do this in the future.
Like :- 36, 54, 81’s M.S. ,
First of all 36 and 54 M.S. Removed by this method.
36) 54 (1)
36
18) 36 (2)
36
Hence H.S.M. of 36 and 54 is = 18
Now, the H.P. of 18 and 81 is Let’s take it out.
18) 81 (4
72
9) 18 (2
18
×
Hence the H.M.S. of 36, 54 and 81 is 9 is
L of decimal numbers S. and m. S. Removal
Write all the given decimal numbers in the form of rational number p/q and find their LCM on the basis of fractions. or m.s. Let’s know.
Like :- 7, 10.5 and 1.4’s m. S.
So 7 = 7/1, 10.5 = 105/10, 1.4 = 14/10
M.S. = 7 , 105 H.M.S. of 14/1 , 10 , LCM of 10 = 7/10 = 0.7
H.C.M. of fractions and L.S.P. ,
- H.C.M. of fractions = H.C.M. of numerator/L.C.M. of denominator.
- LCM of fractions = LCM of numerator/LCM of denominator
Formulas for greatest common factor and least common factor :
- Least Common Factor of Fractions (L.C.M) = LCM of Fractions/LCM of Denominators
- Highest Common Factor of Fractions (H.C.F.) = H.C.M. of Fractions/L.C.M. of Denominators
- L.S. × M.S. = first number × second number
- L.S. = (1st number × 2nd number) ÷ M.S.
- M.S. = (1st number × 2nd number) ÷ L.S.
- First number = (LCM × HCM) ÷ Second number
- second number = (lcm × mcm) ÷ first number
Read More : LCM and LCM
3. Formula of BODMAS rule
The process of converting a mathematical expression into an ordinary fraction or numerical form is called ‘Simplification’
Under this, solving mathematical operations like addition, subtraction, multiplication, division etc. on the basis of BODMAS order, the value of the given expression is obtained.
There are four types of brackets –
― → Line Bracket
( ) → Simple or Small Bracket
{ } → Curly Bracket
[ ] → Square Bracket
Simplify them in this order.
If there is a minus sign before the parentheses, then all the signs inside are changed on simplification.
Rule of BODMAS :- In BODMAS, the operations of Bracket, Of, Division, Multiplication, Addition, and Subtraction are done simultaneously.
Therefore, to solve the questions related to BODMAS, solve the questions in the order given above, that is, first do the action of Bracket.
In Bracket first line bracket ( – ) then small bracket ( ) then middle bracket { } then big bracket [ ] solve.
Then the operation of (of), then the operation of division (÷), then the operation of multiplication (×) and finally the operation of subtraction, there is no change in the order if one or more of the above operations are absent.
B → Bracket Line bracket, small bracket, middle bracket, large bracket
O → Of
D → Division
M → Multiplication
A → Addition
S → Subtraction
4. Simplification
Apart from the above sequence, various algebraic formulas are also used in the simplification of expressions.
Important Identities of Simplification :
Common factor : c(a + b) = ca + cb
Square of Binomial :
- (a+b)² = a² + 2ab + b²
- (a-b)² = a² – 2ab + b²
Product of sum and difference of two terms: a² – b² = (a+b) (a-b)
Other identities (sum and difference of cubes) :
- a³ – b³ = (a – b) (a² + ab + b²)
- a³ + b³ = (a+b)(a² – ab + b²)
Cube of Binomial :
- (a + b)³ = a³ + 3a²b + 3ab² + b³
- (a – b)³ = a³ – 3a²b + 3ab² – b³
Square of the polynomial :
- (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
Multiplication of two binomials with a common term : (x + a )(x + b ) = x² + (a + b )x + ab
Gauss’s identity : a³ + b³ + c³ – 3abc = (a+b+c) (a² + b² + c² – ab -bc – ca)
Legendre identity :
- (a+b)² + (a-b)² = 2(a² + b²)
- (a+b)² – (a-b)² = 4ab)
- (a+b)4 – (a-b)4 = 8ab(a² + b²)
Lagrange’s identity :
- (a² + b²) (x² + y²) = (ax+by)² + (ay-bx)²
- (a² + b² + c²) (x² + y² + z²) = (ax+by+cz)² + (ay-bx)² + (az-cx)² + (bz-cy )²
5. Formulas of square and square root
- √ab = √a × √b
- (ab)1/2 = √ab = (a)1/2 × (b)1/2
- √a/b = √a/√b
- (ab)1/2 = √a/b = a1/2b1/2
- (a+b)2 = a2 + 2ab + b2
- (a-b)2 = a2 – 2ab + b2
- (a+b)2 + (a-b)2 = 2(a2 + b2)
- (a+b)2 – (a-b)2 = 4ab)
- (a+b)4 – (a-b)4 = 8ab(a2 + b2)
If n is any positive integer, then
(n + 1)² – n² = ( n + 1 + n ) ( n + 1 – n )
= ( 2n + 1 )
यथा
(6)² – (5)² = (2 × 5 + 1)
= 11
The square of a two digit number with 5 in its unit’s place is done as follows.
(25)² = 2 × 3 (hundreds) + 52
= 2 × 300 + 25
= 625
And
(35)² = 3 × 4 (hundreds) + 52
= 3x 400 + 25
= 1225
6. Formula of Average
The ‘average’ of two or more like terms is the number obtained by dividing the sum of the given terms by the number of those terms. It is also called ‘median’.
Average = sum of all zodiac signs/number of zodiac signs
Sum of all zodiac signs = Average × Number of zodiac signs
Like :- x1 , x2 , x3 , . , , , , , Average of xn terms = x1 + x2 + x3 + . , , , , , xn/n
- Average of first n natural numbers = (n+1)/2
- Average of natural numbers up to n = (n+1)/2
- Average of consecutive whole numbers up to n = n/2
- Average of even numbers up to n = (n+2)/2
- Average of consecutive natural odd numbers up to n = (n+1)/2
- Average of odd numbers up to n = n
- Average of n consecutive even numbers = n+1
- Average of squares of first n natural numbers = (n+1) (2n+1)/6
- Average of cubes of first n natural numbers = n(n+1)² / 4
- Average = (First Number + Last Number) / 2
- Age of new person = (new average × new number) – (old average × old number)
- If the average of quantities G₁ and G₂ are A₁ and A₂ respectively, then the average of quantities (G₁+G₂) = (G₁×A₁) + (G₂×A₂) / (G₁ + G₂).
- If the average of quantities G₁ and G₂ are A₁ and A₂ respectively, then the average of quantities (G₁ – G₂) = (G₁×A₁) – (G₂×A₂) / (G₁ – G₂).
7. Discount Formula
Generally, when a trader sells something to his customer, he gives some discount on the marked price, this discount is called discount, the general meaning of discount is discount.
Note: Discount is always given on marked price.
Selling price = Marked price – Discount
If a discount of r% is being given on selling an article, then
Selling price of article = Marked price × (100-r)/100
Important facts of discount :
1. If a discount of r% and R% is being given on the marked price of an article, then
Selling price of the article = Marked price × (100 – r) / 100 × (100 – R) / 100)
2. If the two discount rates are r% and R%, then
The equivalent discount will be (r + R – rR/100)%.
3. If a profit of R% is to be obtained even after giving a discount of r% on an article, then
Marked price of article = cost price × [(100 + R) / (100 – r)
4. If a profit of R% is to be obtained even after giving a discount of r% on an article, then
The marked price of the article will be increased by [(r + R / 100 – r) × 100].
5. Marked price = Selling price × 100 / (100% – %) × 100 / (100% – %) 100 / (100% – %)……….
6. Selling price = Marked price × (100% – %)/100 × (100% – %)/100 × (100% – %)/100× ……….
8. Percentage Formulas
meaning of percent (per + cent) per hundred or x out of 100 percent meaning x out of 100
x% = x/100
To convert the fraction x/y to a percentage, multiply the fraction by 100.
x/y part of an item = (x/y) × 100 of that item
- y percent of x = x × y 100
- x is what percent of y = x/y × 100
- By what percent is y more than x = (y – x)/x × 100
- By what percent is y less than x = (x – y)/x × 100
- percent increase = increase/initial value × 100
- percent decrease = decrease/initial value × 100
- Increasing x by R %, we get x(1 + R/100)
- Subtracting R % from x, we get x(1 – R/100)
Other Important Formulas :
- Finding the new number when x is increased by y % = (100 + y)/100 × x
- If the value of x is R% more than y then the value of y is less than x in R% = R/(100 + R × 100)%
- If the value of x is R% less than y then the value of y is R% more than x = R/(100 – R × 100)%
- To ensure that the total expenditure on the article does not increase even if the price of an article is increased by R%
- R% decrease in consumption of commodity = R/(100 + R × 100)%
- To ensure that the total expenditure on the article does not decrease even if the price of an article is reduced by R%
- R% increase in consumption of commodity = ( R/(100 – R× 100)%
- If A = x × y then percentage change in A due to m% change in x and n% change in y = m + n + mn/100
- Where + sign will be used for increase and – sign for decrease.
Formula based on population :
Let the population of a city be x and it increases at the rate of R% per annum, then
Population after n years = x [1 + R/100]ⁿ
Population n years ago = x [1 + R/100]ⁿ
Regarding depreciation of machines:
If the present value of an article is x and its rate of depreciation is R% per annum, then
Value of the machine after n years = p(1 – R/100)ⁿ where + sign is used for increase and – for decrease.
Cost of machine n years ago = p/(1 + R/100)ⁿ
| 5% | 1/20 |
| 10% | 1/10 |
| 20% | 1/5 |
| 25% | 1/4 |
| 30% | 3/10 |
| 40% | 2/5 |
| 50% | 1/2 |
| 60% | 3/5 |
| 70% | 7/10 |
| 75% | 3/4 |
| 80% | 4/5 |
| 90% | 9/10 |
| 100% | 1 |
9. Formulas of profit and loss
Cost Price :- The price at which an article is bought is called the cost price of that article.
Selling Price :- The price at which an article is sold is called the selling price of that article.
Profit :- If the selling price of an article is more than its cost price, then the amount received from their difference is called profit.
Loss :- If the selling price of an article is less than its cost price, then the amount received from the difference is called loss.
Percentage profit or percentage loss: – The amount of profit or loss on 100 rupees is called percentage profit or loss. The percentage of profit or loss is always determined on the cost price.
- Profit = Selling Price – Cost Price
- loss = cost price – selling price
- selling price = profit + cost price
- Selling Price = Cost Price – Loss
- cost price = selling price – profit
- cost price = loss + selling price
- Profit % = (Profit × 100)/Cost Price
- Loss % = (Loss × 100)/CP
- Selling Price = Cost Price (1 + Profit/100)
- Cost Price = Selling Price / (1 + Profit / 100)
- Selling Price = Cost Price(1 – Loss/100)Cost Price = Selling Price/(1 – Loss/100)
10. Formulas of Ratio and Proportion
Ratio :- The relation between two quantities/objects of the same type is called ratio.
The ratio of two quantities is equal to a fraction, so it shows how many times one quantity is less or more than the other quantity.
Let one quantity be x and the other quantity be y, then the ratio between them = x : y
Type of Ratio :-
Mean ratio between x and y = √x. y
Third ratio between x and y = y²/x
Inverse ratio of x and y = 1/x : 1/y = y : x
The mixed ratio of two equal ratios is called square ratio.
Like :- Square ratio of a : b = a² : b²
The square root of a ratio is called square root proportional.
Like :- square root of a : b = √a : √b
The third power of a ratio is called the cubic proportional.
Like :- Cube ratio of a : b = a³ : b³
The cube root of a ratio is called the cube root proportion.
Like :- Cube root of a : b = ∛a : ∛b
The inverse of a proportion is called inverse proportion.
Like :- Inverse proportion of a : b = 1/a : 1/b
When two ratios are equal to each other, they are said to be proportional.
For example :- a : b = c : d, then a, b, c and d are proportional
Invertendo is a ratio which changes places.
Like :- Inverse proportion of a : b = c : d is b : a :: d : c
i.e. a/b = c/d or b/a = d/c
11. Formulas of Simple Interest
- Interest = (Principal × Time × Rate)/100
- compound = principal + simple interest
- Compound = Principal × (100 + Rate of Interest times)
- Principal = Compound – Simple Interest
- Principal = Simple Interest × 100 / Time × Rate of Interest
- Time = Simple Interest × 100 / Principal × Rate of Interest
- Rate of interest = SI × 100 / Principal × Time
- Compound = Principal × (100 + Time × Rate)
12. Compound Interest Formula
- Compound interest = (1 + rate / 100 )^time – principal
- Compound Interest = Principal [(1 + Rate / 100)^times – 1]
- compound interest = compound – principal
- The mix is calculated as follows.
- Compound = Principal × (1 Rate / 100)^Time
- compound = principal + interest
13. Mensuration Formulas
(i). Triangle ∆ (Triangle) :
- Area of equilateral triangle = √3/4 × (side)²
- Perimeter of equilateral triangle = 3 × side
- Length of the perpendicular drawn from the vertex of an equilateral triangle = √3/4 × side
- Area of isosceles triangle = 1/4a√4b² – a²
- Perimeter of an isosceles triangle = a + 2b or a + 2c
- Length of perpendicular drawn from vertex A of isosceles triangle = √(4b² – a²)
- Perimeter of a scalene triangle = sum of all three sides = a + b + c
- Half perimeter of triangle S = ½ × (a + b + c)
- Area of scalene triangle = √s(s – a)(s – b)(s – c)
- Area of right angled triangle = ½ × base × altitude
- Perimeter of right triangle = Perpendicular + Base + Hypotenuse = a + b + c
- Hypotenuse of a right triangle = √(perpendicular)² + (base)² = √(c² + a²)
- Altitude of right angled triangle = √(hypotenuse)² – (base)² = √(b² – a²)
- Base of right triangle = √(hypotenuse)² – (perpendicular)² = √b² – c²
- Area of isosceles right triangle = ¼ (hypotenuse)²
- On multiplying each side of a triangle by x, the perimeter becomes x multiplied and the area x² multiplied.
- Each angle of an equilateral triangle is 60°.
- The sum of the three angles of a right triangle is 180°, that is, two right angles.
(ii). Rectangle :
- Area of rectangle = length × breadth
- Diagonal of rectangle =√(length² + breadth²)
- Perimeter of the rectangle = 2(length + breadth)
- If there is a path inside a rectangular field, then the area of the path = 2 × width of the path × [(length of the field + width of the field) – (2 × width of the path)]
- If there is a path outside the rectangular field, then the area of the path = 2 × width of the path × [(length of the field + width of the field) + (2 × width of the path)
(iii). वर्ग (Square) :
- Area of square = (a side)² = a²
- Area of square = (perimeter)²/16
- Area of square = ½ × (product of diagonals) = ½ × AC × BD
- Perimeter of square = 4 × a
- Diagonal of square = a side × √2 = a × √2
- Diagonal of square = √2 × area of square
- Perimeter of square = diagonal × 2√2
- If a path is made all around the outside of the square area, then the area of the path = 4 × width of the path (one side of the square area + width of the path)
- If a path is made all around inside the square area, then the area of the path = 4 × width of the path (one side of the square area – width of the path)
(iv). Cube :
- Volume of cube = a × a × a
- Volume of cube = (one side)³
- one side of a cube 3√volume
- Diagonal of cube = √3a cm.
- Diagonal of cube = √3 × one side
- One side of cube = Diagonal/√3
- Perimeter of cube = 4 × a × a
- Total surface area of the cube = 6 a² square Centimeters.
(v). Cylinder :
- Volume of cylinder = πr²h
- Curved surface area of cylinder = 2πrh
- Total surface area of the cylinder = (2πrh + 2πr²h) square centimetres.
- Area of both surfaces = 2πr²
- Volume of hollow cylinder = πh(r²1 – r²2)
- Curved surface of hollow cylinder = 2πh(r1 + r2)
- Total surface area of hollow cylinder = 2πh(r1 + r2) + 2π (r²1 – r²1)
(vi). Cone :
Curved surface area of cone = πrl
Surface area of cone = πr(r + l)
Volume of cone = (πr²h)/3 cm.
Slant height (l) = √(r² + h²)
Height of cone (h) = √(l² – r²)
Radius of cone (r) = √(l² – h²)
Total surface area of the cone = (πrl + πr²) square centimetres.
(vii). Frastrum of Cone :
Volume of frustum of cone = (πh)/3 (R² + r² + Rr)
Area of the slant = π (R + r)³, l² = h² + (R – r)²
Total surface area of frustum = π[R² + r² + l(R + r)]
Slant height = √(R – r)² + h²
(viii). Trapezium Quadrilateral :
- Area of trapezium = ½ × sum of parallel sides × distance between parallel sides
- Area of trapezium = ½ × height × sum of parallel sides
- Area of trapezium = ½ × h × (AD + BC)
- Perimeter of parallelogram = 2 × (Sum of adjacent sides)
- Area of rhombus = ½ × product of diagonals
- Perimeter of rhombus = 4 × one side
- Area of a quadrilateral = ½ × one diagonal
- One side of rhombus = √(diagonal)² + (diagonal)²
- One diagonal of rhombus = √side² – (second diagonal/2)²
- Area of regular hexagon = 6 × ¼√3 (side)²
- Area of regular hexagon = 3√3×½ (side)²
- Perimeter of regular hexagon = 6 × side
- side of hexagon = radius of circumcircle
- Number of diagonals of a regular polygon of n sides = n(n – 3)/2
(ix). Cuboid :
- size of face of cuboid = rectangle
- There are 6 faces or faces in a cuboid.
- A cuboid has 12 edges.
- A cuboid has 8 vertices.
- Volume of cuboid = length × breadth × height
- length of cuboid = volume/(breadth × height)
- Breadth of cuboid = Volume/(Length × Height)
- Height of cuboid = Volume/(Length × Breadth)
- Volume of cuboid = l × b × h
- Perimeter of cuboid = 2(l + b) × h
- Area of all the faces of cuboid = 2(Length × Breadth + Breadth × Height + Height × Length)
- Total surface area of cuboid = 2(lb + bh + hl)
- Diagonal of cuboid = √(length)² + (breadth)² + (height)²
- Diagonal of cuboid = √l² + b² + h²
- Total surface area of the open box = length × breadth + 2(width × height + height × length)
- Area of four walls of the room = 2 × height × (length + breadth)
- Maximum length of the rod that can be placed in a room = √(length)² + (breadth)² + (height)²
(x). Sphere :
- Volume of sphere = (4πr³)/3 cubic centimeter
- Curved surface area of sphere = 4πr² square centimeter
- Radius of sphere = ∛3/4π × volume of sphere
- Diameter of sphere = ∛ (6 × volume of sphere)/π
- Volume of spherical shell = 4/3π(R³ – r³)
- Total surface area of sphere = 4πr
- Radius of sphere = √Total surface/4π
- Diameter of sphere = √Total surface/π
- Volume of spherical shell = 4/3π(R³ – r³)
(xi). Semipsphere :
- Curved surface area of hemisphere = 2πr²
- Volume of hemisphere = 2/3πr³ cubic centimeter
- Total surface area of hemisphere = 3πr² square centimeter
- Radius of hemisphere is r, then volume of hemisphere = 2/3 πr³
- Total surface area of hemisphere = 3πr²
(xii). CIRCLE :
- Diameter of circle = 2 × radius = 2r
- Circumference of circle = 2π Radius = 2πr
- Circumference of circle = π × diameter = πd
- Area of circle = π × radius² = πr²
- Radius of circle = √Area of circle/π
- Perimeter of semicircle = (n + 2)r = (π + 2)d/2
- Area of the semicircle = 1/2πr² = 1/8 πd²
- Area of sector = θ/360° × Area of circle = θ/360° × πr²
- Perimeter of sector = (2 + πθ/180°)r
- Area of sector = (πθ/360° – 1/2 sinθ)r²
- Perimeter of sector = (L + πrθ)/180°, where L = length of chord
- Arc length = θ/360° × circumference of the circle
- Arc length = θ/360° × 2πr
- Area between two concentric circles whose radii are R1, R2, (R1 ≥ R2) = π(r²1 – r²2)
(xiii). Volume Formulas :
volume of cube = side³
Volume of cuboid = length × breadth × height
Volume of cylinder = πr²h
Volume of hollow cylinder = π(r1² – r2²h)
Volume of cone = ⅓ πr2h
Volume of frustum of cone = ⅓ πh[r1² + r2²+r1r2]
Volume of sphere = 4/3 πr3
Volume of hemisphere = ⅔ πr3
Volume of spherical shell = 4/3 π(r13 – r23)
14. Time Distance and Speed Formulas
Speed :- The distance traveled by a person/means of transport in unit time is called speed.
Formula of speed = speed = distance / time
Unit of Speed : The unit of speed is meter/centimeter or kilometer/hour.
If the speed is in metres/centimetres, then
- kilometer/hour = 18/5 × meter/centimeter
If the speed is in kilometer/hour, then
- meter/centimeter = 5/18 × kilometer/hour
Distance :- The distance covered by a person/means of transport to change the place is called.
Formula of Distance :- Distance = Speed × Time
Time : The distance traveled by a person/means of transport at a unit speed determines its time.
Formula of time :- Time = distance / speed
Relative Speed :- If two objects are moving at a speed of km/h and b km/h respectively, then
- If both are in opposite direction, then relative speed = (a + b) kilometer/hour
- If both are in same direction, then relative speed = (a – b) kilometer/hour
Train and Platform :- When a train crosses a long object/place (platform/bridge/another train), then along with its length, the train has to cover an additional distance equal to the length of that object. have to do,
Means total distance = length of rail + length of platform/bridge
15. Algebra Formulas
- (a + b)² = a² + 2ab + b²
- (a + b)² = (a – b)² + 4ab
- (a – b)² = a² – 2ab + b²
- (a – b)² = (a + b)² – 4ab
- (a + b)² + (a – b)² = 2(a² + b²)
- (a + b)² – (a – b)² = 4ab(a + b)³ = a³ + 3a²b + 3ab² + b³
- (a + b)² – (a – b)² = a³ + b³ + 3ab(a + b)
- (a – b)³ = a³ – 3a²b + 3ab² – b³
- (a – b)³ = a³ + b³ + 3ab(a + b)
- (a + b)³ + (a – b)³ = 2(a³ + 3ab²)
- (a + b)³ + (a – b)³ = 2a(a² + 3b²)
- (a + b)³ – (a – b)³ = 3a²b + 2b³
- (a + b)³ – (a – b)³ = 2b(3a² + b²)
- a² – b² = (a – b)(a + b)
- a³ + b³ = (a + b)(a² – ab + b²)
- a³ – b³ = (a – b)(a² + ab + b²)
- a³ – b³ = (a-b)³ + 3ab(a – b)
- (a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
- (a + b + c)³ = a³ + b³ + c³ + 3 (a + b)(b + c)(c + a)
- a³ + b³+ c³ = (a + b + c)³ – 3(a + b)(b + c)(c + a)
- (a + b + c + d)² = a² + b² + c² + d² + 2(ab + ac+ ad + bc + bd + cd)
- a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ca)
- x² + y² + z² – xy – yz – zx = ½[(x – y)² + (y – z)² + (z + x)²]
- a³ + b³ + c³ – 3abc = ½(a + b + c) [(a – b)²+(b – c)²+(c – a)²]
- a² + b² + c² – ab – bc – ca = ½[(a – b)²+(b – c)²+(c – a)²]
- a(b – c) + b(c – a) + c(a – b)=0
- ab(a – b) + bc(b – c) + ca(c – a) = -(a – b)(b – c)(c – a)
- a²(b² – c²) -b²(c² – a²) +c²(a² – b²) = (a – b)(b – c)(c – a)
- a + b = (a³ + b³)/(a² + ab + b²)
- a – b = (a³ – b³)/(a² + ab + b²)
- a + b + c = (a³ + b³ + c³ – 3abc)/(a² + b² + c² – ab – bc – ca)
- (a + 1/a)² = a² + 1/a²+2
- (a² + 1/a²) = (a + 1/a)²-2
- (a – 1/a)² = a² + 1/a²-2
- (a² + 1/a²) = (a – 1/a)²+2
- (a³ + 1/a³ = (a+1/a)³-3(a+1/a)
- (a³-1/a³ = (a-1/a)³-3(a-1/a)
16. Formulas of Trigonometry
Right Triangle Law
- (hypotenuse)² = (perpendicular)² + (base)²
- (perpendicular)² = (hypotenuse)² – (base)²
- (Base)² = (Hypotenuse)² – (Perpendicular)²
Trigonometric Ratios
- sinθ = perpendicular / hypotenuse
- cosθ = base/hypotenuse
- tanθ = perpendicular / base
- cotθ = base/perpendicular
- secθ = hypotenuse / base
- cosecθ = hypotenuse /perpendicular
trigonometric relations
- sinθ.cosecθ = 1
- cosθ.secθ = 1
- tanθ.cotθ = 1
- tanθ = sinθ/cosθ
pythagorean formula
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = cosec²θ
trigonometry formulas
- sin(A – B) = sinA.cosB – cosA.sinB
- cos(A + B) = cosA.cosB – sinA.sinB
- cos(A – B) = cosA.cosB + sinA.sinB
- tan(A + B) = (tanA + tanB)/(1 – tanA.tanB)
- tan(A – B) = (tanA – tanB)/(1 + tanA.tanB)
- sin2A = 2sinA.cosA
- cos2A = cos2A – sin2A = 2cos2A-1 = 1 – 2sin2A
- tan2A = 2tanA/(1 – tan2A)
Trigonometry Table
| θ | 0 | 30°= Π/6 | 45°= Π/4 | 60°= Π/3 | 90°= Π/2 | 180°= Π | 270°= 3Π/2 | 360°= 2Π |
| sinθ | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cosθ | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tanθ | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cosecθ | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| secθ | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| cotθ | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
17. Formulas of Integration
- ∫xⁿ∙dx = x⁽ⁿ⁺¹⁾/(n+1) + C
- ∫ex∙dx = ex + C
- ∫e-x∙dx = -e-x + C
- ∫1/x∙dx = log x+ C
- ∫Sin x∙dx = – Cos x + C
- ∫Cos x∙dx = Sin x + C
- ∫Tan x∙dx = log Sec x + C
- ∫Cot x∙dx = log Sin x + C
- ∫Sec x∙dx = log |Sec x + Tan x | + C
- ∫Cosec x∙dx = log |Cosec x – Cot x | + C
- ∫1/√(1 – x²)∙dx = Sin-1 x + C
- ∫1/(1 + x²)∙dx = Tan-1 x + C
- ∫1x(√x² – 1)∙dx = Sec-1 x + C
- ∫1√(a² – x²)∙dx = Sin-1 (x/a ) + C
- ∫1√(x² – a²) ∙dx = log | x + √(x² + a²) | + C
- ∫1√(x² – a²) ∙dx = log | x + √(x² + a²) | + C
- ∫√(a² – x²) ∙dx = x/2 √(a² – x²) + a²/2 Sin-1 ( x/a ) + C
- ∫√(a² + x²)∙dx = x/2 √(a² + x²) + a² /2 log | x + √(x² + a²) | + C
- ∫√(x² – a²)∙dx = x/2 √(x² – a²) – a²/ 2 log | x + √(x² – a²) | + C
- ∫1/(a² – x²)∙dx = ½ a log | (a + x)/(a – x)| + C
- ∫1/( (x² – a²)∙dx = ½ a log | (x – a)/(x + a)| + C
- ∫Sec² x∙dx = Tan x + C
- ∫Cosec² x∙dx = – Cot x + C
- ∫Sec x ∙ Tan x∙dx = Sec x + C
- ∫Cosec x ∙ Cot x∙dx = – Cosec x + C
- ∫K∙dx = Kx + C (Where K = Constant Quantity)
- ∫1/(x² + a²)∙dx = 1/a Tan1 x/a + C
18. Differentiation Formulas
- dxⁿ/dx = n xⁿ – 1
- d(Sin x)/dx = Cos x
- d(Cos x)/dx = – Sin x
- d(Tan x)/dx = Sec 2x
- d(Cotx)/dx = – Cosec 2x
- d(Sec x)/dx = Sec x ∙ Tan x
- d (Cosec x)/dx = – Cosec x ∙ Cot x
- d(sin-1x)/dx = 1/√(1 – x²)
- d(cos-1x)/dx = 1/(√1 – x²)
- d(tan-1x)/dx = 1/(1 + x²)
- d(Cot-1x)/dx = 1/(1 + x²)
- d(Sec-1x)/dx = 1/x√x² – 1
- d(Cosec-1x)/dx = 1/x√x² – 1
- d ex/dx = e x
- d e-x/dx = – e x
- d log x/dx = 1/x
- d ax/dx = a x log x
- d √x/dx = ½ √x
| Read More : | ||
| Roman Numbers 7 to 700 | Squares from 7 to 700 | Cube Table 7 to 40 |
| Roman Numbers 7 to 7000 | Square Root 7 to 700 | Cube from 7 to 700 |
Hope you have liked the information about Mathematics Formula in English.
If you liked this information, then definitely share this article with your friends.